Dit principe is eenvoudig te
demonstreren aan een buis die zich in zijn loop vernauwt. Daar
waar de buis nauwer wordt zal de vloeistofstroom sneller zijn.
Dit laat zich vertalen in de volgende formule:
Vloeistoffen verschillen fundamenteel van gassen en vaste stoffen. Eén van de eigenschappen van vloeistoffen waar we gebruik van kunnen maken is de incompressibiliteit. Dit betekent dat het volume van een vloeistof niet door uitwendige druk vergroot en verkleind kan worden. Dit wetende is het dus te begrijpen dat bij iedere instroom van vloeistof in een ruimte, dit gecompenseerd moet worden door een even grote uitstroom van vloeistof uit diezelfde ruimte.
Dit principe is eenvoudig te
demonstreren aan een buis die zich in zijn loop vernauwt. Daar
waar de buis nauwer wordt zal de vloeistofstroom sneller zijn.
Dit laat zich vertalen in de volgende formule:
A1 v1 = A2 v2
Het product van de snelheid (v) waarmee de vloeistof door een buis met oppervlakte (A) van een dwarsdoorsnede stroomt blijft constrant. Dit product van stroomsnelheid en oppervlakte van de dwarsdoorsnede wordt ook wel volumestroom of debiet genoemd. Het meest bekende debiet is het hartminuutvolume. In formulevorm ziet het er als volgt uit:
Q = A v |
De volumestroom wordt uitgedrukt in m3/s. |
Een andere eigenschap van vloeistof is dat vloeistof cohesie en adhesie vertoont door de aantrekkingskracht van ieder molecuul vloeistof op een ander molecuul vloeistof. Het gevolg van cohesie is dat vloeistof die stil staat, meegesleurd wordt door bewegende vloeistofmoleculen. Adhesie wordt gedemonstreerd door het feit dat als iemand zijn hand in een vat met vloeistof steekt er altijd druppels vloeistof aan de hand kleven als deze wordt teruggetrokken; niet alle vloeistof valt terug.
Wanden van een bloedvat staan stil, anders gezegd de snelheid van de wand van een vat is 0. De laag vloeistofmoleculen die direct tegen de wand van het vat liggen, nemen dus ook zo goed mogelijk de snelheid van die wand over en liggen dus bijna stil. De laag daar net binnen zal weer iets sneller kunnen stromen etc. Uiteindelijk vinden we de snelste moleculen in het midden van het vat. Daarbij wordt aangetekend dat het snelheidsprofiel een parabolische vorm heeft.
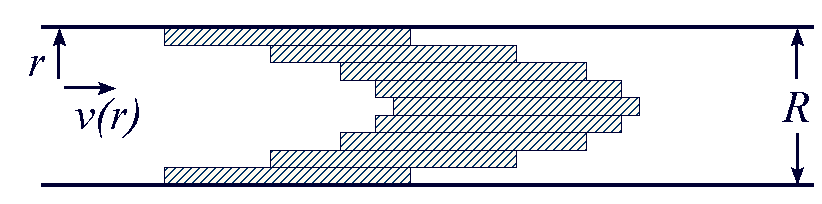
Dit parabolische snelheidsprofiel van bloedstroom wordt laminaire bloedstroom genoemd. Uiteraard wordt er in praktijk meestal gewerk met een gemiddelde stroomsnelheid (Vgem). De volumestroom of debiet in een vat kan uiteindelijk berekend worden met de formule:
 |
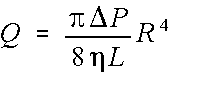Hierbij wordt het product van pi en het
drukverschil gedeeld door het product van 8, viscositeit en de lengte van de buis waarover het drukverschil gemeten is, maal de straal van het vat tot de 4e macht. We kunnen nu concluderen dat:
|
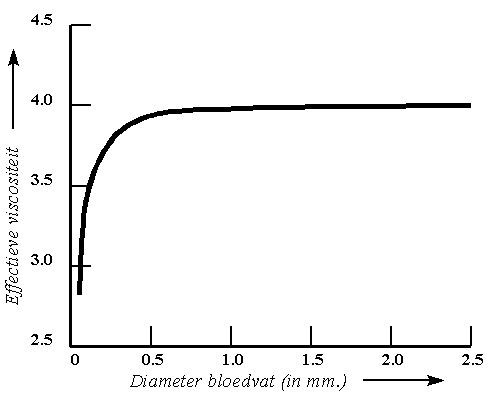
Uit de bovenstaande formule is dus af te leiden dat de bloedstroom in de capillairen nogal traag zal zijn. Het blijkt echter dat de volumestroom in de capillairen onverwacht hoger is dan op grond van de bovenstaande formule te verwachten is. Deze grotere volumestroom wordt veroorzaakt door een afname van de viscositeit in de kleinere vaten. Dit effect wordt het Fåhraeus-Lindqvist effect genoemd. Het Fåhraeus-Lindqvist effect wordt veroorzaakt een eigenschap van bloedcellen, te weten Rouleaux vorming. Hierbij worden de rode bloedcellen als het ware gestapeld.
|
 |
|
| Rouleaux vorming van erytrocyten | Viscositeit bloed uitgezet tegen de diameter van een vat |
Hierboven hebben we gezien dat de bloedstoom zich in principe laminair met een parabolisch snelheidsprofiel door de bloedvaten beweegt. In praktijk zal de bloedstroom echter vaak turbulent zijn. Turbulentie wordt veroorzaakt door de traagheid van de vloeistofmoleculen. In hoeverre deze traagheid de laminaire stroming verstoort wordt uitgedrukt in het dimensieloze getal van Reynolds (Re).
 |
 |
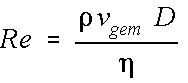Aangezien de soortelijke weerstand van het bloed en de viscositeit van het bloed grootheden zijn die afhangen van de vloeistof zelf, wordt de mate van turbulentie voornamelijk bepaald door de diameter van het bloedvat en de gemiddelde stroomsnelheid van het bloed door het vat. Bij een grotere diameter, of een hogere bloedstroomsnelheid zal er dus eerder turbulentie optreden. Experimenteel blijken de volgende waarden van het Reynolds getal van belang te zijn:
Uit een simpele rekensom volgt dat in de aorta een Reynolds getal van ongeveer 1000 geldt en in een capillair van ongeveer 0.001. Turbulentie speelt dus in de normale circulatie geen grote rol van betekenis. Dit verandert in pathologische situaties bij stenose door bijvoorbeeld vasoconstrictie of atherosclerose, waar wel op beperkte schaal turbulentie op kan treden.
Over het algemeen is turbulentie een ongewenst effect. Omdat bij turbulentie stromingen in diverse richtingen optreden (dit in tegenstelling tot een laminaire stroming) is de stroming minder efficient. Hierdoor treedt een verhoging van de hydrodynamische weerstand op, waarbij over hetzelfde drukverschillen kleinere volumestroom het gevolg is.
* Tekst vrij overgenomen uit Biomedische Wetenschappen Vorm en Functie 1992
